One of my mentors gave me several books he'd found valuable as a machinist, before he became an engineer.
One is a neat book called Design and Use of Cutting Tools, by Leo St. Clair, all about cutting tool geometry. The most important factors for tool life are correct rake and relief angles, so the book describes several methods of measuring angles. Let's back up a bit:
In school you may have heard of the small angle approximation, which says that as an angle gets very close to zero radians, the sine of that angle is approximately equal to the angle. This is why the equation for the period of a pendulum that you get in high school physics has the big caveat that "this only applies at small angles". (The small angle approximation can be demonstrated with the Taylor series expansion of sine; as the angle gets close to zero, the higher ordered terms drop out and you're left with sine=theta.)
As a corollary to this, cosine equals one at small angles. This can be derived by taking the Taylor series expansion of cosine; as the angle approaches zero, the higher ordered terms drop out and you get cosine=one.
So we know that at small angles sine is about equal to theta, and cosine is about equal to one. And we remember that sine over cosine is tangent. We can then make the reasonable assumption that for small enough angles, the tangent ought to be equal to the angle. Or linear with the angle, anyway.
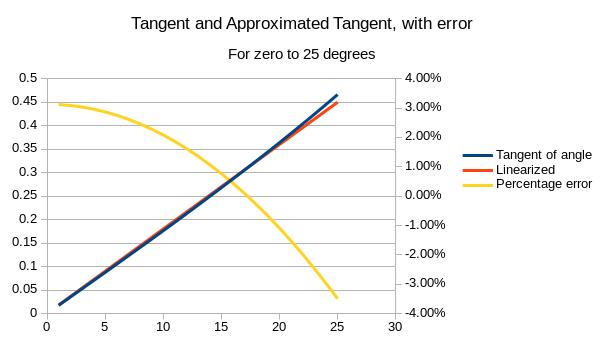
Back to tools: we need to measure angles, and all we've got are rulers. We could try some really fancy trigonometry (like land surveyor level stuff), but the angles are all relatively small with cutting tools, so all that small angle business still just screw up the numbers. However, Mr. St. Clair comes to the rescue with the small angle approximation. He shows that between 0° and 20°, the tangent of the angle is approximately equal to the angle (in degrees) times .018. Within this range, the tangent will be correct to within 1/3rd of a degree, which is pretty good. But since we have spreadsheets, which Leo St. Clair probably didn't have in 1953, we can double-check his math.
One is a neat book called Design and Use of Cutting Tools, by Leo St. Clair, all about cutting tool geometry. The most important factors for tool life are correct rake and relief angles, so the book describes several methods of measuring angles. Let's back up a bit:
In school you may have heard of the small angle approximation, which says that as an angle gets very close to zero radians, the sine of that angle is approximately equal to the angle. This is why the equation for the period of a pendulum that you get in high school physics has the big caveat that "this only applies at small angles". (The small angle approximation can be demonstrated with the Taylor series expansion of sine; as the angle gets close to zero, the higher ordered terms drop out and you're left with sine=theta.)
As a corollary to this, cosine equals one at small angles. This can be derived by taking the Taylor series expansion of cosine; as the angle approaches zero, the higher ordered terms drop out and you get cosine=one.
So we know that at small angles sine is about equal to theta, and cosine is about equal to one. And we remember that sine over cosine is tangent. We can then make the reasonable assumption that for small enough angles, the tangent ought to be equal to the angle. Or linear with the angle, anyway.
Back to tools: we need to measure angles, and all we've got are rulers. We could try some really fancy trigonometry (like land surveyor level stuff), but the angles are all relatively small with cutting tools, so all that small angle business still just screw up the numbers. However, Mr. St. Clair comes to the rescue with the small angle approximation. He shows that between 0° and 20°, the tangent of the angle is approximately equal to the angle (in degrees) times .018. Within this range, the tangent will be correct to within 1/3rd of a degree, which is pretty good. But since we have spreadsheets, which Leo St. Clair probably didn't have in 1953, we can double-check his math.
What I did was plot the tangent function from zero to 25 degrees, and then plot Leo St. Clair's approximation (.018 x theta), and the percentage error. From the plot, we can see that .018 times theta is within about 3% of the real tangent for angles up to 25 degrees. So there you have it! Up to 25 degrees, you can safely linearize tangent, and all your mental math becomes much simpler.
 RSS Feed
RSS Feed